高沢公信"Critique"/2003.5.20

情報を編集することの効果２
〜アナロジーをどう見つけるか１〜

情報を編集することの効果１〜アナロジー発見効果
情報を編集することの効果３〜アナロジーをどう見つけるか２
情報を編集することの効果４〜アナロジーをどう見つけるか３
情報を編集することの効果５〜アナロジーをどう使うか

　新しい構成の発見に導くアナロジーをどうやって手に入れたらいいのか？ゴードンは，『シネクティクス』の中で，アナロジーの手法を，

・擬人的類比（personal analogy）

・直接的類比（direct analogy）

・象徴的類比（symbolic analogy）

・空想的類比（fantasy analogy）

　の４つ挙げている。直接的類比は，対象としているモノを見慣れた実例に置き換え，類似点を列挙していこうとするものであり，擬人的類比は，対象としているテーマになりきることで，その機構や働きのアイデアを探るという，いわゆる擬人法であり，象徴的類比は，ゴードンの取り上げている例では，インドの魔術師の使う伸び縮みする綱のもつイメージを手掛かりに連想していこうとするものであり，空想的類比は，潜在的な願望のままに，自由にアイデアをふくらませていこうとするものであるが，いずれも，その区別はわかっても，それをどう使いこなし着想に結びつけるかの方法論は具体化されていない。もちろん，擬人法や空想は，アナロジーの手掛かりとして重要であるのは，後述する通りであるが，こういうアナロジーの分類だけではアナロジー発見の手掛かりとはなりにくい。

　むしろ，大事なのは，アナロジーの発想の仕組み（アナロジーの見方）であり，類似性と関係性というアナロジーの構造（アナロジーの見え方）をはっきりさせることだ。

•  アナロジーの仕組み

　では，アナロジーはどんな構造をしているのか,その共通した仕組みをまずはっきりさせておかなくてはならない。前述したように，アナロジーの中身は，関係性と類似性であるから，その違いから，アナロジーと概括されるものを，以下のように２つにわけることができる。

　・類似性に基づくアナロジーを，｢類比｣

　・関係性に基づくアナロジーを，｢類推｣

　既に類似性と関係性で触れたように，前者は，内容の異質なモノやコトの中に形式的な相似(形・性質など），全体的な類似を見つけだすのに対して，後者は，両者の間の関係（因果・部分全体など）を見つけ出す。関係性に基づくアナロジー＝類推を整理すると，

・構成要素の関係性からの類推

・関係から見えてくる全体構造の類推

の２つのタイプがある（類似性に基づくアナロジー＝類比は，後で触れるように，類推の特殊型なのである）｡

• 両者の構成要素のもつ関係性からの類推

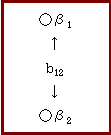
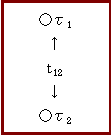
　第１は，典型的には，独立した２つの対象間の構成要素の対比によって，下図のように，既知のＢの要素間(β₁β₂)の関係(b₁₂)がわかっており，Ｔの要素(τ₁)とＢの要素(β₁)とが対応し，ＢとＴの要素間の関係（b₁₂とt₁₂）が対応しているとき，それとの類推から，Ｔにおいてもτ₂があるに違いない，と推測していく。

　この場合，要素の類推だけでなく，関係そのもの（b₁₂，t₁₂）の類推でもいいし，またこの場合，性質が１つであれば類比となる。この意味からみれば，類似性に基づく類比は，対比する両者の比較項目を１として括ったときに成立する，特殊なアナロジーなのである。

Β　　　　              　　　　　　Ｔ

　さらに，関係性に基づくアナロジーの場合は，厳密に言えば，Ｂ→Ｔの全体同士，β₁→τ₁，β₂→τ₂，……β_n→τ_nの要素間の１対１の対応関係と，Ｂとその構成要素β₁，β₂,……β_n，Ｔとその構成要素τ₁，τ₂，……τ_nといった関係，とは異なる関係性をもっている。前者を，水平関係，後者を垂直関係，と呼ぶこともできる。例えば，原子と太陽系の比較で言えば，核と太陽，電子と惑星といった１対１の関係とは別に，原子構造→電子・核，太陽系→惑星・太陽の間には，全体・部分乃至因果関係を見ることができる。あるいは，次の例で言えば，

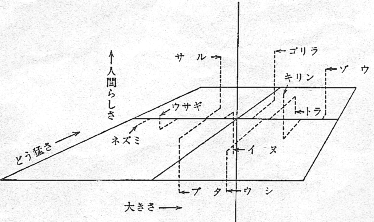
                                       出典;M.ﾍｯｾ著『科学･モデル･アナロジー』(培風館)

　と，対比した場合，水平関係（の１対１の関係）では類似性が見られ，垂直関係（の全体と構成要素の関係）では全体・部分の関係がみられる。当然，比べる両者の間に，水平関係の対応があれば，ある程度まで垂直関係が類推できることになる。

《類似性による空間の再構成》

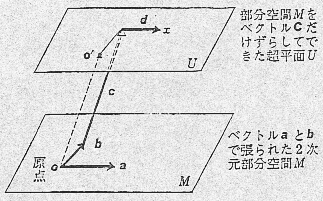
《類推による世界の再構成》

出典;右図は,佐伯胖著『イメージ化による知識と学習』(東洋館出版社),左図は,ﾙｰﾒﾙﾊｰﾄ著『人間の情報処理』(ｻｲｴﾝｽ社)

 　また，ここでは２次元での関係の比較をしているが，これが３次元での関係あってもいいし，コトを考えるとき，時間経過を考えることも当然ありうるのである。

例えば，３次元空間に，部分集合の間の親疎を，距離をもとに位置づけて，各部分集合は「ｍ次元の類似性空間内に，それぞれ一個の点として表現できる」とし，それらの関係は，座標の中に，それぞれの間の方向と距離で表現されるとしてみたり（ルーメルハート），「韓国の産業構造は， 数年前のわが国の産業構造である」といった類推や比喩表現を，｢部分空間｣との“ずれ”（平行とは限らない）によって形成された「空間」に，元の空間の関係を“転移"（置き換え）することで推測していくものとして，表現しようとする考え方（佐伯胖）等々がある（上図）。

いずれも，各要素間の関係を，座標軸上の距離（奥行や幅）や方向をもってプロットしようとするもので，上述したところに奥行の関係を加えただけで，基本的には同じである。

(以下続く)

アナロジーについては，ここを御覧下さい｡
アナロジーの見つけ方については，ここをご覧下さい｡
アナロジーの見方チェックリスト，アナロジーの見え方チェックリスト参照下さい｡