高沢公信"Critique"/2002.5.20 |
|
発想できる仕掛けをつくる-1- 頭を柔らかくするとは,ある意味では自分を変えることだ。しかし,そんなに簡単に自分が変えられるなら,世話はない。発想というのは,自分を変えることではなく,自分が変わることなのだ。自分を変えるから発想ができるのではなく,そういう発想ができるから自分が変わるのだ。だから,発想の仕掛けとは,自分のモノの見方を変えるのではなく,モノの見方が変わる(変わらざるをえない)仕掛けを作ることだ。
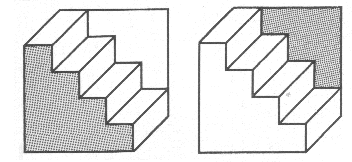
9点の課題に対するエイコフ等の試みのもつ意味を一層明らかにしてくれるのは,シュレーダーの階段と呼ばれるものである。
出典;種村季弘・高柳篤『だまし絵』(河出文庫) まず,右側の図を見てほしい。前方から見たとき,別の向きの階段が見えるだろうか?見えなかったら,逆さにしてみてほしい。すると,もう一つ別の方向の階段が見えてくるはずである。右図は,わかりやすいために,手前を少し色を変えてある。左の図は,それをさらにわかりやすくするために,奥のところを色を変えてある。つまりねもうひとつの階段が見つかりやすくしてある。 この例で言いたいのは,見ている対象を転倒させる(見え方を変える)だけで,知っているものに,別のものが見えてくる,ということだ。あるいは見知らない,違ったものとして見えてくる。そうすることで別の見方ができる。別の見方をしたかったら,見え方を変えればいい。見え方を変えるには,モノの在り方を変えればいいのである。これを整理すれば, 在り方を変える→見え方が変わる→とらえ方が変わる ↑ ↓ ↓ 在り方が変わる←見え方を変える←とらえ方を変える と図式化することができよう。つまり,われわれは,見えるものの在り方を変えることによって見え方を変えてしまう,そして見え方を変えることでそのとらえ方を変えてしまうことができる。エイコフやアダムスがしていたことの意味は,このように与えられた課題の条件を変えることで,その見え方を変え,別の見方を可能にすることだったのである。 このことはしかし,われわれが日常的にやっていることではなかろうか。例えば,モノの正体がわからないとき,それを逆さにしたり裏返したり,目に近づけたり遠ざけてかざしたりすかしたりしているが,そうやって見えているモノを動かすことで,結果としてわれわれは,無意識にいつもの見方を変えているのである。 ただ,ここで注意すべきなのは,9点にしろシュレーダーの階段にしろ,これはモノそのものではなく,(いずれも文字や図解された)モノの情報にすぎないという点だ。厳密に言えば,モノの見え方を変えるには, ①モノそのものを動かす ②モノを見る媒介を変える ③モノについての情報を動かす の3つがありえるはずである。②の媒介とは,顕微鏡や望遠鏡によって小さいもの(遠いもの)を大きく見たり,偏光レンズによって2次元画像を立体画像に見たり,というものである。しかし,これも高速度カメラにとらえたフィルム画像と同様に,一種のわれわれの視覚レベルへの変換情報と考えれば,③に一括することができる。 こうしてモノとモノの情報と2つに整理してみると,われわれが日常,情報を通してモノを見,情報を通してモノを考え,判断もしている(厳密に言えば,感覚情報,知覚情報自体がそうだ)ということを思い知らされるのである。その意味では,モノと情報の区別ははっきりしなくなっているのである。 しかし,既に述べたところからも明らかなように,われわれの発想において,ものの見方・とらえ方を枠づけているのは,知識・経験というわれわれ自身のもっている情報を含め,われわれが絶え間なく接している,言葉,映像,画像,記号,表情,論理,イメージその他,ありとあらゆる情報なのだ。そして,9点の課題のように,その見え方を変えなければ,われわれは見方を変えにくいのである。その意味で,発想を問題とする本書では,見え方というとき,主として情報の見え方という意味で使うつもりである。見え方が変わる→とらえ方が変わる,というのは,情報の見え方を変えることで情報の見方が変わる,という意味になる。といって,それがモノとイコールになるわけではないから,直接モノ(コト)に当たれば見え方が変わることは少なくない。しかし,それは情報の見え方を変える条件の1つと見なせばいいのではあるまいか。
見え方を変える例として,ジグソーパズルを考えてみる。ジグソーパズルは,小片に分解されたチップを組み合わせて,元の画像を復元していく。しかし,そのためには,何の手掛かりもなしに作業をしているのではない。つまり, ・大きい形だと,元の形を知識・経験から想像しやすい, ・絵柄がついていれば,情報の方向(視野)が一定になり,画像のイメージから完成図を予想 しやすい, ・枠組があれば,輪郭(再現の目標=モデル)がある, と,ある程度の大きさがあったり,図柄があるから全体像を予想しやすいし,輪郭があるから,そこから逆算して組み合わせパターンを推定しやすいのであり,輪郭や図柄が組み合わせの手掛かりになる。しかし,もし, ①小片がそれぞれの区別がつかないくらい小さい ②小片の裏と表の区別がない(図柄がない) ③再現すべき輪郭がない という条件になったらどうなるであろうか?見慣れたものにまとめていく(当てはめていく)手掛かりがなくなると,どの組み合わせも見慣れない,異質なものになってしまうのである。つまり, ①小片がちいさければ小さいほど復元は難しくなる(情報にカタチが見えない) ②小片の裏と表の区別がなくなると復元が難しい(情報に方向が見えない) ③枠組をなくしてしまうと復元が難しい(情報に目標が見えない) のであり,それは,見え方は,対象を細分化するほど,全体の位置も意味も文脈も見分けのつかないものになってしまうということを意味している。 こうして分解され,細分化されることで,見慣れた見え方でなくなるということは,こうしたものの組み合わせもまた,見慣れない,異質なものにしてしまうのではあるまいか?とすれば,“異質な組み合わせ”は,外から探して来るのではなく,その組み合わせ要素を細分化し,見慣れないものにすることによっても可能なのではあるまいか。 もう少し,別の例で考えてみる。例えば,初めての場所へ行くのにおおまかな地図を知りたいと情報を集める場合,雑誌や知人等々,あっちこっちから細切れの情報を収集し,それを図解しながら,まとまった地図に仕上げていく。それは,図解すれば, 情報を集める(あっちこっちからかき集め) ↓ 情報を観察する(あれこれ眺め) ↓ 情報を組み合わせる(分類・整理する) といったステップになる。多少不案内だと,経験者やガイドブツクを頼って断片をかき集めることになるが,よく知っているところなら,このステップは省略され,自分の記憶から引き出された情報を組み合わすだけで,作成可能である。このいずれの場合も,もう少し順序立てて考えると,次のような手順を踏むはずだ。 ①バラバラの情報集め, ②それをメモのように見える形にし, ③それをつなぎ合わせたり,組み合わせたりして, ④更にそれを図解などして, ⑤求める正解(現実の復元)を達成しようとする。 しかし,こうして情報を組み合わせても創造性とは言わない。なぜなら,これは,どこかにある現場(=正解)を再現しようとしているだけだからだ。したがって,こういう場合,集められる情報は,現実の復元可能な,同一レベルの質をもったものでなければならない。もしこれが,全然違った形で与えられたとしたらどうか。例えば, (様式)図解,チャート,平面図,俯瞰図,立体図,暗号,数式 (形態)細かくする→もっと細かくする→元が分からない位細分化する(視点)他の道筋,いろんなの人の見方,もっとこまかな見方,悪意の情報,無知の情報 (条件)過去の地図,道路情報,未来の区画整理予定表,夜の情報,朝の情報 と,種類も形式も全くのバラバラだったとしたら,おそらく再現は不可能に近いはずだ。ジグソーパズルで見たように,情報は細かくなるほど,また多様な,多角的な情報が加わるほど,再現がしにくくなり,ついには,事実からはなれて,単なる無意味なデータ,言葉になりやすい。これではとうてい,元の枠組は再現不可能で,まったくでたらめな組み合わせにならざるをえない。だが,それを無意味と取るのではなく,生かすかたちで使えるはずなのだ。つまり,細分化するほど,
とは,見慣れた見え方が変わったことを意味している。それは,情報のもっている,どんな視点(誰が,どこから)で,どういう様式・形態(どういうように)に,何を(その意味),どういう条件(状況)で,という基本要件を崩すことにほかならない。あるいは見えているものの,形状・意味,向き (どこから),状況,といった基本要件を崩すと言い換えても同じである。それは,ジグソーパズルで見たように,①ものの枠組をなくすこと ②部分を細分化してしまうこと ③視覚の方向をなくしてしまうこと によって,既知の脈絡ではまとめにくくなり,別に脈絡を見つけ出すような組み合わせをせざるを得なくなる。
しかし,いくら見え方を変えるためとは言っても,ただひたすら小さくするだけでいいのだろうか? 細分化は確かに,見え方を崩しはするが,それがただ同一・同型の小片に小さくするだけであれば,逆に,それをまとめるために既知の枠組に頼らざるをえなくなるだろう。積木が現実のモノをなぞる,真似ることになるのは,大体同型の立方体になっているからだ。小片そのものに,何の手掛かりもなければ,結局自分の知識・経験をなぞるしかない。とすると,細分化とは,むやみに小さくすることだけではない。言葉で言えば,五十音に分解してしまえば,その言葉は積木の一片と同様,情報としての意味を失う(それを組み合わすのは,例えば,猿にキイボードをランダムに叩かせて,文章をまとめさせようというのに近い)。とすれば,少なくとも,細分化とはいっても,その限界は,意味をなす最小単位ということでなくてはならない(「あ!」のように1音でも意味をもつものはもちろんあるが)。 そこから,もう一言つけ加えれば,見え方を変えるのは,何も物理的に分解することだけではないということだ。例えば,幾何の問題を解くとき,補助線を1本引くだけで,図形が別の見え方になり,解く手掛かりを手に入れられたように,ここでの分解とは,ひとまとまりに見えていたものの形を崩せるものであれば,解体しなくてもいいのである(だから,ここでは,ただ形の細分化だけではなく,後述するように,同じものでも視点や条件によって意味や見え方がさまざまに変わるという意味で,異質化と呼びたい)。必要なのは,いままでの見え方をを崩すことなのである。例えば,日本語では,五七五と語句を切るだけで誰でもが一種の“うた”の見え方を手に入れられるが,山頭火のように,自由俳句と呼ばれるものは,その“うた”の見え方をつくっている定型(五七五)を崩す(いわば字余りだらけにするといった)ことで,新しい見え方を示してみせたのだといっていい。これも,解体ではなく,補助線を引いたのに等しい。 (以下続く) 【目次】へ |